jest stroną towarzyszącą serii książek wydawanych przez AIUT pod wspólnym glównym tytułem
"Fizyka Mojej Urojonej Czasoprzestrzeni", których autorem jest Henryk Dot.
Fizyka 3 - Maxwell
Od autora
Spis treści
O czym jest ta książka
Fragmenty historii
Elementy nowe
Całkowicie błędne
Elementy błędne
Fizyka 3 - Rozdzial 1
Równania
Zespolone pole E i B
Dalsze uogólnienie
Rozwiązanie ogólne
Fizyka 3 - Rozdzial 2
Rozwiązania równań
Warunki początkowe
Równanie niejednorodne
Rozw. dla trzech kierunków
Cztery prawa fizyki
Fizyka 3 - Dodatek
Dowód Fermata
Przypuszczenie Beala
Trójki pitagorejskie
Masa inercyjna
Stała grawitacji big G
Gdzie patrzy Księżyc
Fizyka 3 - Zakończenie
Zakończenie
Fizyka 4 - Przejście do Fizyka 4
Otwarcie nowej książki
"temat" musi zaczynać się od
cyfry reprezentującej aktualny
dzień tygodnia (niedziela=7)
Książki wydawane przez AIUT znajdują się
w bibliotekach zgodnie z listą egzemplarzy obowiązkowych.
Drugie wydanie "Fizyka 3"
ISBN 978-83-926856-1-6

można kupić w Warszawie
w Księgarni Akademickiej
Oficyny Wydawniczej PW
ul.Noakowskiego 18/20
oraz w Katowicach
w księgarni "Liber"
ul. Bankowa 11.
(teren Uniwersytetu Ślaskiego)
Wydanie angielskie "Physics"
ISBN 978-83-926856-2-3

jest również w bibliotekach
a o sposób dystrybucji należy pytać wydawca@aiut.com.
|
3.4. Dlaczego Księżyc nie „patrzy” na Słońce
W czasie 1 i 3 kwadry, kiedy Księżyc jest wysoko nad horyzontem a Słońce nisko 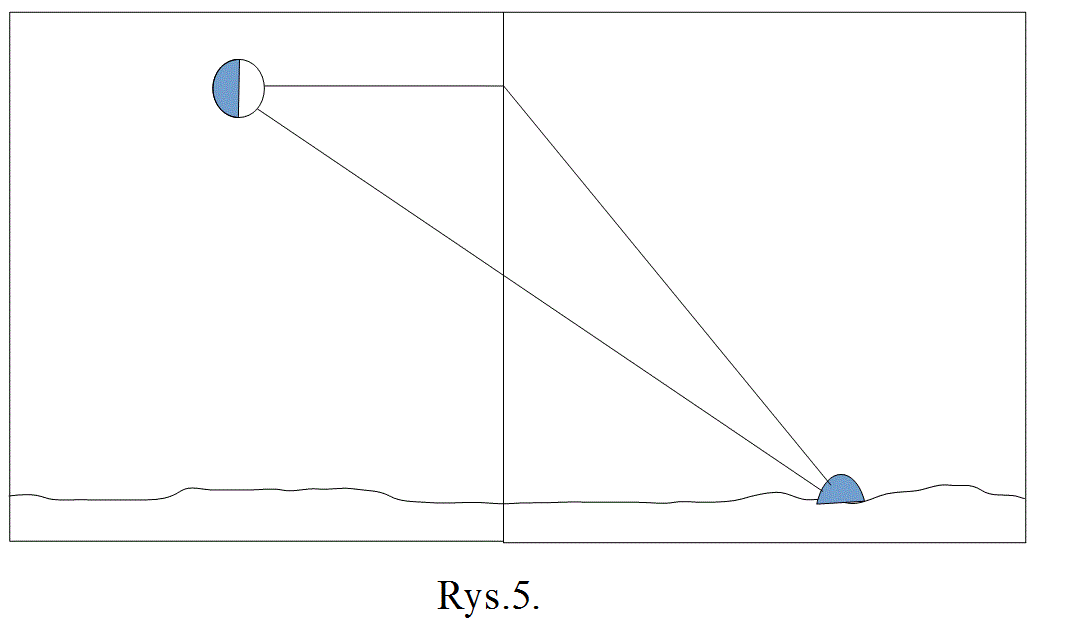
Mimo że jest to obrazek przedstawiany na poziomie szkoły podstawowej, to można na nim pokazać różnicę kątową między rzeczywistym i pozornym promieniem słonecznym. Aby zobrazować drogę promieni słonecznych do Księżyca, wyobraźmy sobie, że łączymy sztywną prostą rurą Słońce i Księżyc. Jest oczywiste, że promienie słoneczne dochodzące do Księżyca muszą biec wewnątrz tej rury. Praktycznie, z uwagi na dużą różnicę średnic tych ciał, będzie to ścięty stożek, ale przy jednoczesnej podobnej różnicy odległości byłby on widoczny prawie jak rura jednakowej średnicy. Nasze zadanie sprowadza się teraz do pytania – jak wyglądałby obraz tej rury na zdjęciu? W tym celu wpierw wykonamy zdjęcie panoramiczne, czyli przeniesienie obrazu sfery niebieskiej na walcowy pionowy ekran E wokół obserwatora co ilustrują poniższe rysunki. 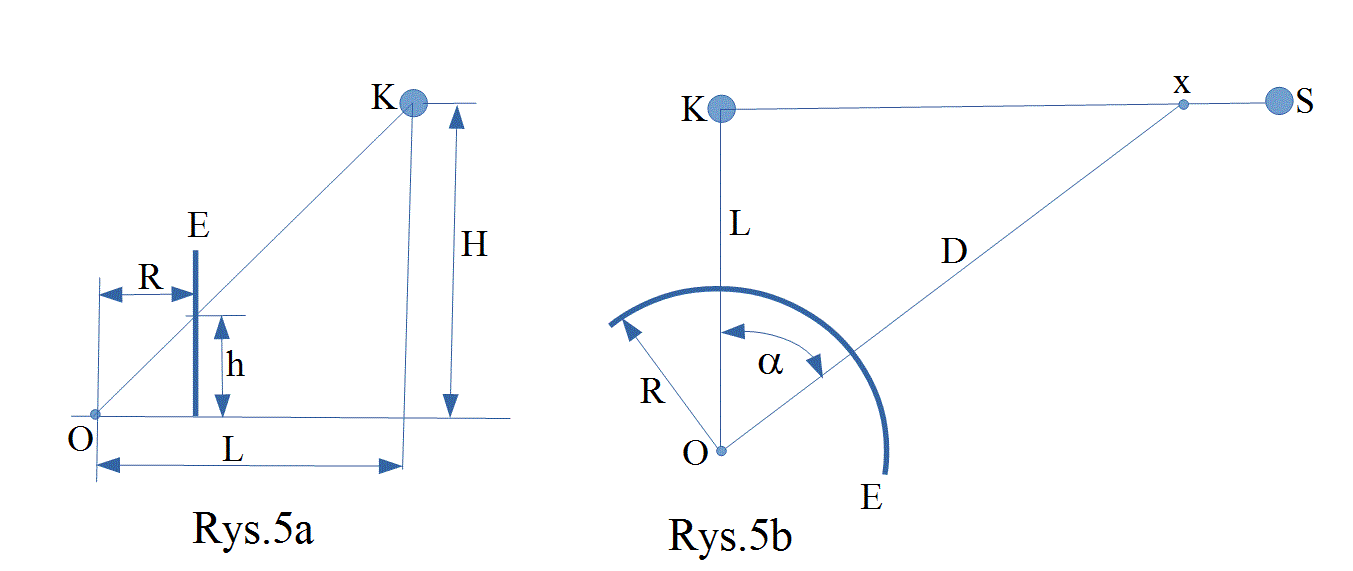
Rysunek 5a pokazuje płaszczyznę przechodzącą przez Księżyc i pion obserwatora O. Rysunek 5b pokazuje płaszczyznę prostopadłą do pionu obserwatora O stanowiącą poziom odniesienia. W czasie I kwadry kąt OKS wynosi 90 stopni. Linia KS(Księżyc-Słońce) reprezentuje „płot” o wysokości H odległy o L od obserwatora O. Obraz Księżyca K na walcowym ( o promieniu R ) ekranie E znajduje się na wysokości | |
|
| (3.23) |
|
Odległość D do punktu x „umownego” płotu jest równa | |
|
| (3.24) |
|
Punkt odpowiadający na ekranie E górze płotu w punkcie x znajduje się na wysokości | |
|
| (3.25) |
|
Widzimy, że na rozwiniętym na płasko ekranie E, oś „rury” łączącej Księżyc i Słońce
ma kształt funkcji cosinus w obszarze od zera do π/2.
W czasie kwadry kąt α musi być nieco mniejszy od π/2 bo odległość Słońca od Księżyca jest skończona.
Zatem kierunek padania promieni słonecznych na Księżyc jest styczny
do cosinusoidy w punkcie α=0, co zauważalnie różni się od kierunku prostej łączącej widoki Księżyca i Słońca w czasie kwadry,
gdy Księżyc jest w najwyższym położeniu a Słońce na linii horyzontu.
Widzimy, że jest to złudzenie „mierzalne”, które jest często wykorzystywane przy realizacji trików filmowych,
zdecydowanie inne od złudzenia dającego różnicę przedmiotów jednakowych. | |
© 2020 Henryk Dot -
