HenrykDot

★ HenrykDot.com ★
jest stroną towarzyszącą serii książek wydawanych przez AIUT pod wspólnym glównym tytułem
"Fizyka Mojej Urojonej Czasoprzestrzeni", których autorem jest Henryk Dot.

ENGLISH

Strona główna

Fizyka 3 - Maxwell
Od autora
Spis treści
O czym jest ta książka
Fragmenty historii
Elementy nowe
Całkowicie błędne
Elementy błędne

Fizyka 3 - Rozdzial 1
Równania
Zespolone pole E i B
Dalsze uogólnienie
Rozwiązanie ogólne

Fizyka 3 - Rozdzial 2
Rozwiązania równań
Warunki początkowe
Równanie niejednorodne
Rozw. dla trzech kierunków
Cztery prawa fizyki

Fizyka 3 - Dodatek
Dowód Fermata
Przypuszczenie Beala
Trójki pitagorejskie
Masa inercyjna
Stała grawitacji big G
Gdzie patrzy Księżyc

Fizyka 3 - Zakończenie
Zakończenie

Fizyka 4 - Przejście do Fizyka 4
Otwarcie nowej książki

Książki wydawane przez AIUT znajdują się
w bibliotekach zgodnie z listą egzemplarzy obowiązkowych.

Drugie wydanie "Fizyka 3"
ISBN 978-83-926856-1-6
Fizyka

można kupić w Warszawie
w Księgarni Akademickiej
Oficyny Wydawniczej PW
ul.Noakowskiego 18/20

oraz w Katowicach
w księgarni "Liber"
ul. Bankowa 11.
(teren Uniwersytetu Ślaskiego)

Wydanie angielskie "Physics"
ISBN 978-83-926856-2-3
Fizyka

jest również w bibliotekach
a o sposób dystrybucji należy pytać wydawca@aiut.com.


2.3. Rozwiązania dla trzech kierunków 2.3.1. Rozwiązanie dla równania jednorodnego Dla trzech kierunków zamiast mamy
.	(2.76)
Operator nabla do kwadratu zwany laplasjanem być może niesłusznie przestraszył niektórych zainteresowanych rozwiązaniem równań Maxwella. W literaturze możemy znaleźć różne próby rozwiązywania tych równań, które polegają na uproszczeniach lub zakładaniu dodatkowych warunków. Dirac pytał swojego współpracownika czy on myśli algebraicznie, czy geometrycznie? Podobnie do rozumienia podchodził Feynman, który uważał, że rozumieć zagadnienie to znaczy, patrząc na równanie, widzieć nie sposób algebraicznego przekształcania wzoru a jego rozwiązania. Przyjrzyjmy się zatem „geometrycznie” równaniu (2.76). Bez straty szczegółowości możemy opuścić symbol wektora nad F i analizować postać
.	(2.77)
Równanie (2.77) opisuje zachowanie funkcji w punkcie przy braku źródeł w tym punkcie, co możemy zobrazować rysunkiem (Rys.3).

Y r F3 F2 F1 /div>
Rys.3
oznaczenia na rysunku x, y, z – układ współrzędnych r - wektor położenia analizowanego punktu F1, F2, F3 – przykładowe fale (oznaczone podwójnymi grotami) liniami w kolorze czarnym oznaczono fale przechodzące przez punkt, liniami w kolorze niebieskim oznaczono fragmenty tych samych fal, ale nie przechodzące przez punkt. Jednorodne równanie falowe postaci (2.77) obejmuje wszystkie fale przechodzące przez punkt , powstałe w punktach, gdzie równanie (2.1) zawiera źródła fali. Oba człony równania (2.77) zawierają w sobie sumę wszystkich możliwych fal, przy czym ilość tych fal w ogólnym przypadku jest określona przez ilość źródeł, które mogą mieć ciągły rozkład w przestrzeni. Ponieważ mamy do czynienia z liniowym równaniem różniczkowym to równanie musi spełniać suma wszystkich fal jak i każda z fal osobno, co pozwala na zajmowanie się tylko jedną falą (czyli rozwiązaniem) przechodzącą przez dany punkt dla jednego dowolnie wybranego kierunku (przyjmując przykładowo, że na tym kierunku jest jedyne źródło fali). Kierunek możemy oznaczyć jako wˆ = w_x∙ xˆ + w_y∙ yˆ + w_z∙ zˆ , gdzie wˆ , xˆ , yˆ , zˆ – wektory jednostkowe w_x ,w_y ,w_z – składowe wektora jednostkowego wˆ , które spełniają zależność w_x² + w_y² + w_z² = 1 . Oznaczając położenie analizowanego punktu przez r₀⃗ , możemy dla pęku prostych przechodzących przez ten punkt zapisać wszystkie wektory położenia w postaci r⃗ = r⃗ ₀ + ξ ∙ wˆ i odpowiadające im wartość funkcji
.	(2.78)
Dla ustalonych r₀⃗ i wˆ będziemy pisać w skrócie F(r⃗ , τ ) =F_ξ ( ξ , τ ) pamiętając, że funkcja F_ξ ( ξ , τ ) jest określana dla konkretnych ustalonych parametrów r₀⃗ i wˆ . Wprowadzimy jeszcze zmienną R i jej odpowiednik wektorowy R⃗ = wˆ ∙ R , które będą wykorzystane w dalszych wzorach. Wykorzystując nowe oznaczenia mamy 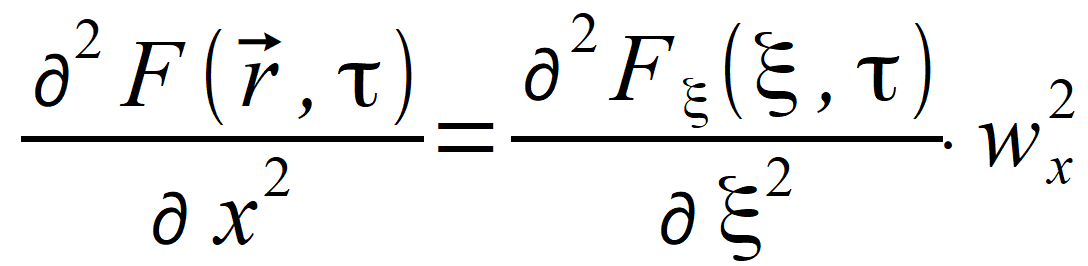, ,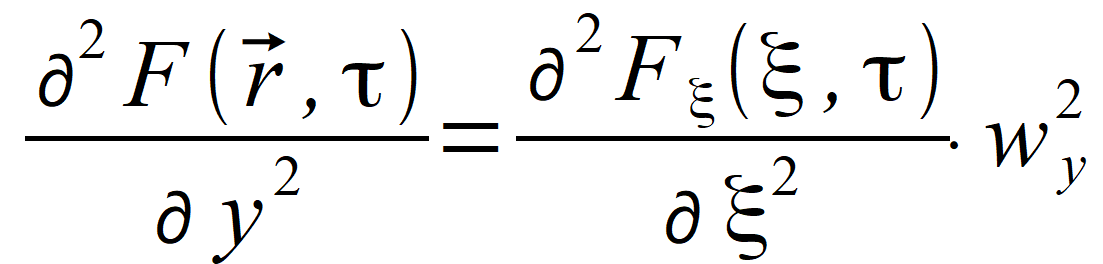 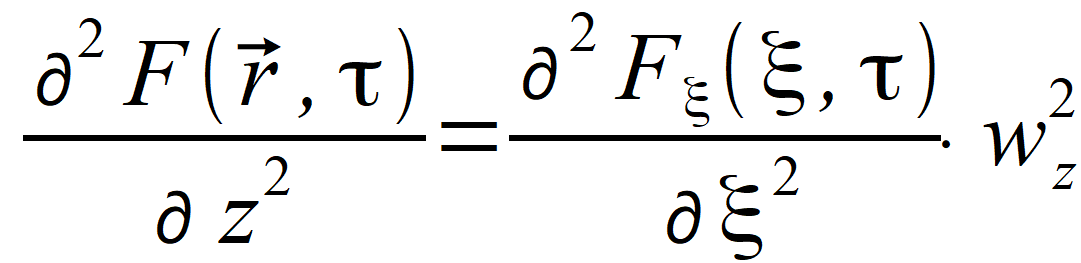i widzimy, że
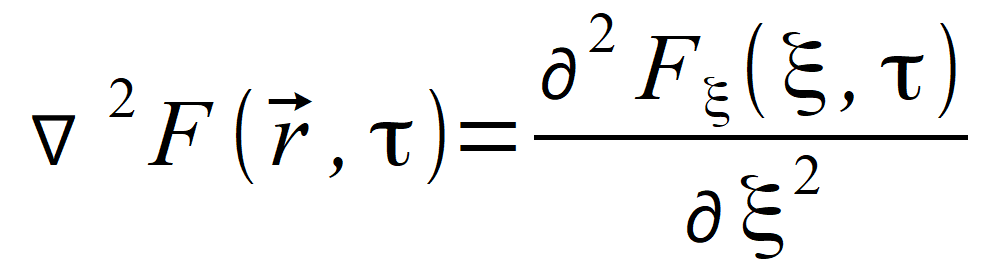	(2.79)
i tym samym nasze równanie w trzech kierunkach stało się już dobrze rozpracowanym równaniem w jednym kierunku
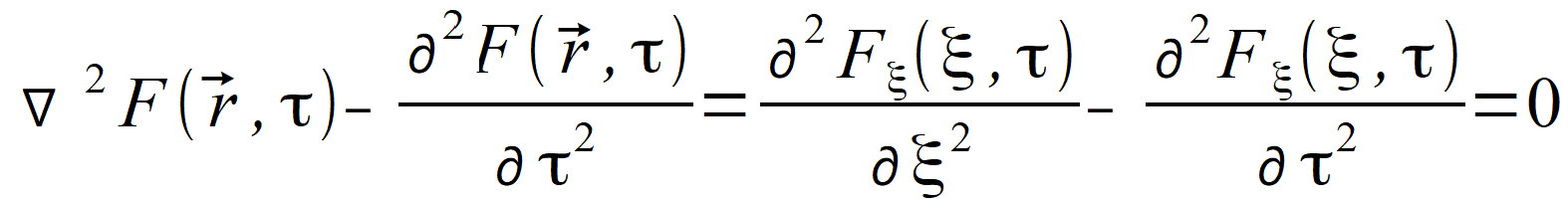	(2.80)
dla którego potrafimy określić rozwiązania. Widząc, że rozwiązanie nie zależy od pozostałych wymiarów, zwykliśmy uważać rozwiązanie dla jednego kierunku za falę płaską. Rozwiązania równania postaci F_ξ ( ξ , τ ), mimo że ma wiele cech podobnych, już za falę płaską uważać nie można, ponieważ określa ono przebieg funkcji tylko na prostej ξ ∙ wˆ przechodzącej przez punkt r⃗ ₀ . Chcąc otrzymać wartość funkcji w punkcie r⃗ ₀ , musimy zsumować wszystkie rozwiązania we wszystkich kierunkach wˆ przechodzące przez punkt r⃗ ₀ . Jeżeli elementarny kąt sferyczny oznaczymy dΩ, to używając miary radialnej kąta mamy
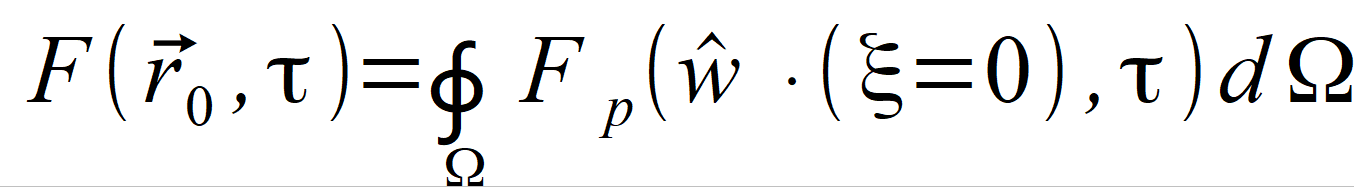	(2.81)
Dolny indeks p w oznaczeniu funkcji F_p ( wˆ ∙ ξ , τ ) oznacza falę przychodzącą na kierunku wˆ i należy przy ustalaniu funkcji F_p ( wˆ ∙ ξ , τ ) uwzględnić wpływ kierunku. W przypadku równań Maxwella wielkość F_p ( wˆ ∙ ξ , τ ) jest wektorem i całka ma postać
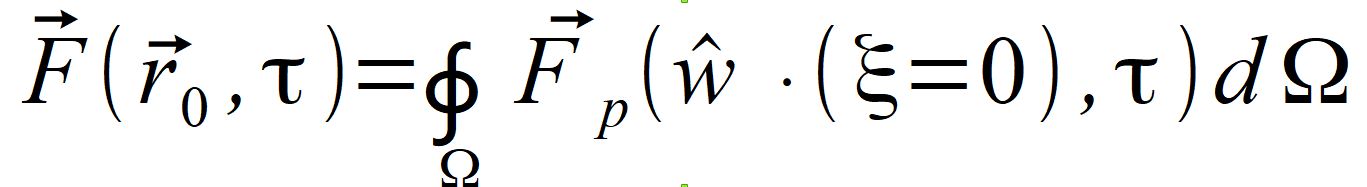	(2.82)
2.3.2. Rozwiązanie równania niejednorodnego Zależności (2.80) i (2.82) pozwalają na konstrukcję rozwiązania dla równania niejednorodnego w trzech kierunkach. Uzupełniając równanie (2.80) o wymuszenia f ( r⃗ , τ ) występujące we wzorze (2.1) działające tylko na wybranym kierunku, czyli f_{w, ξ} ( wˆ ∙ ξ , τ ) otrzymujemy
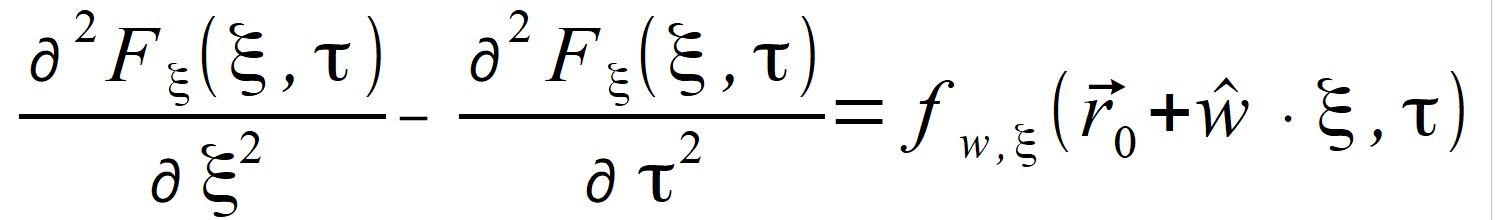	(2.83)
dla którego na wzór (2.74) i (2.75) możemy napisać rozwiązania
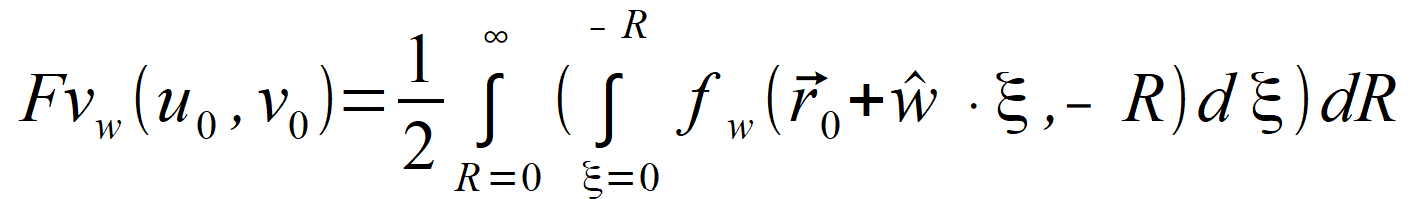	(2.84)
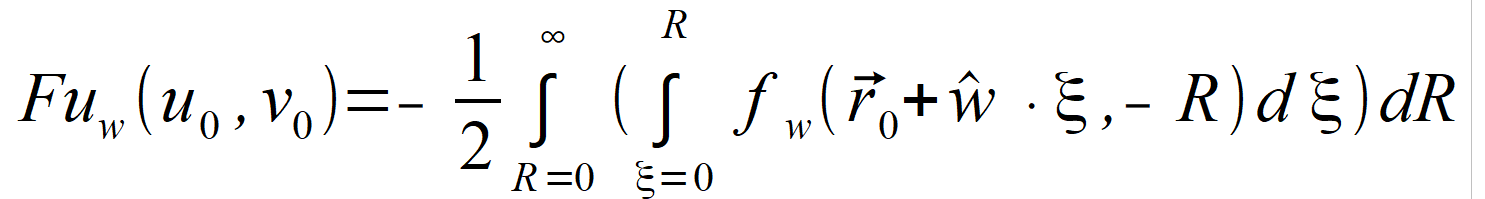	(2.85)
Dla zaznaczenia, że funkcje f ( r⃗ , τ ) , Fv oraz Fu odnoszą się tylko do wybranego kierunku przypisano im dolny indeks w . To samo należy uczynić z funkcją Fo ze wzoru (2.69) przez co otrzymujemy
Fo_w ( u₀ , v₀ ) = Fv_w ( u₀ , v₀ ) + Fu_w ( u₀ , v₀ )	(2.86)
Wewnętrzne całki we wzorach (2.84) i (2.85) są zależne tylko od R. Oznaczając Fo_{w, R} () ich całki nieoznaczone
	(2.87)
wzory (2.84) i (2.85) możemy zapisać
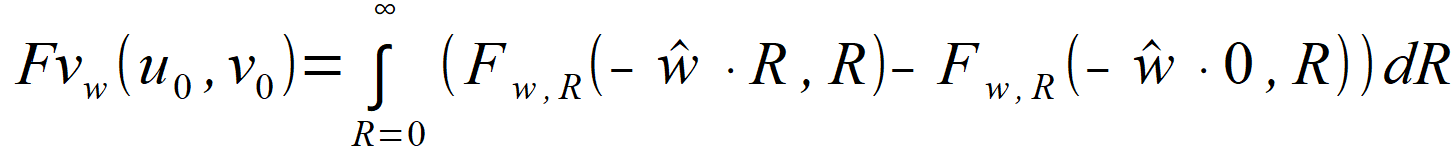	(2.88)
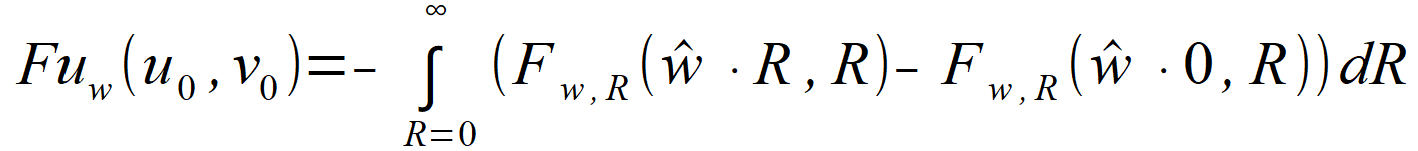	(2.89)
co po uwzględnieniu (2.86) daje
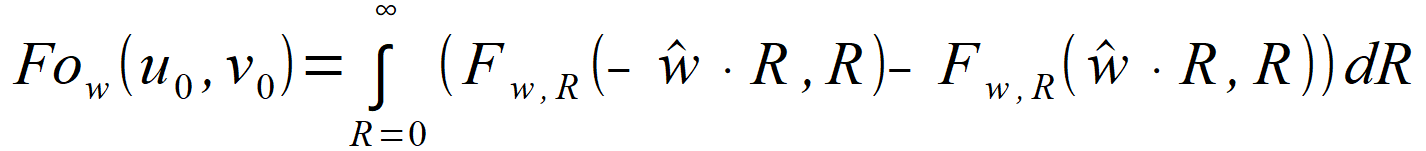	(2.90)
Fo_w ( u₀ , v₀ ) we wzorze (2.90) odpowiada F_p ( r⃗ ₀ + wˆ ∙ ( ξ = 0 ) , τ) we wzorze (2.81). Zauważamy, że 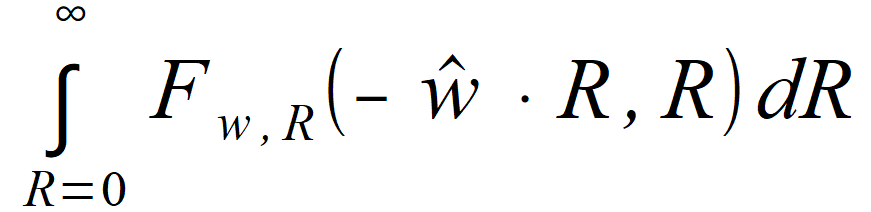oraz 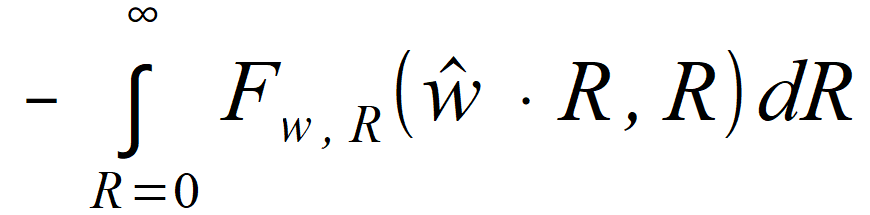są falami przychodzącymi z przeciwnych kierunków i całką fal przychodzących po wszystkich kierunkach jest suma całek po tej samej półkuli 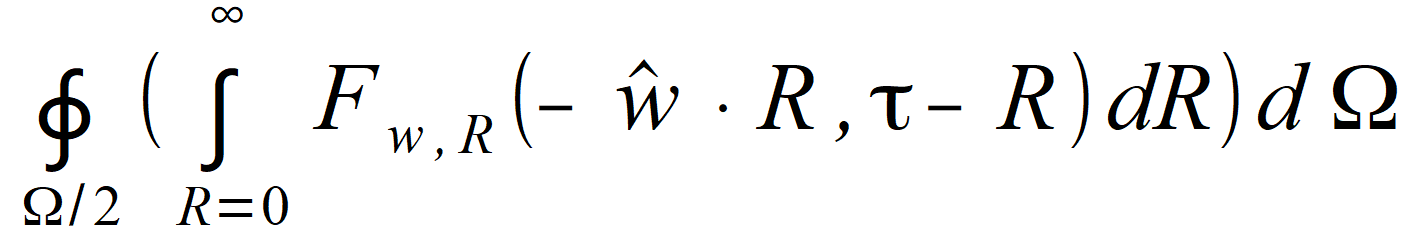dla jednej półkuli 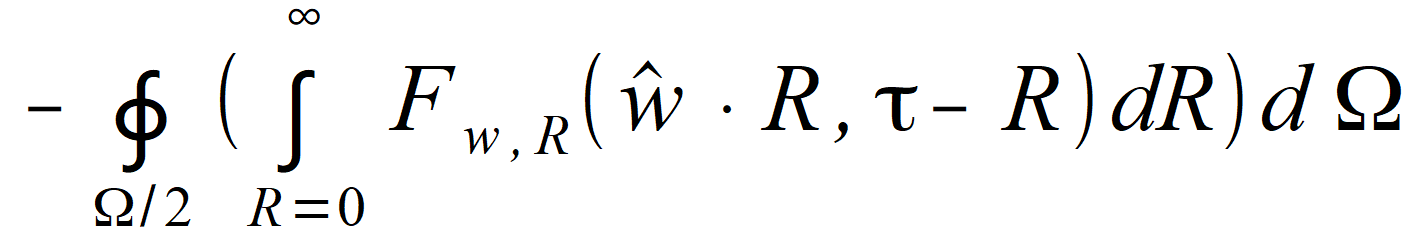i dla drugiej półkuli. Odwrócenie kierunku, czyli zamiana w na -w jest równoważne zmianie znaku całkowania i sumę obu tych całek otrzymujemy, gdy całkować będziemy po całej kuli według jednego ze wzorów
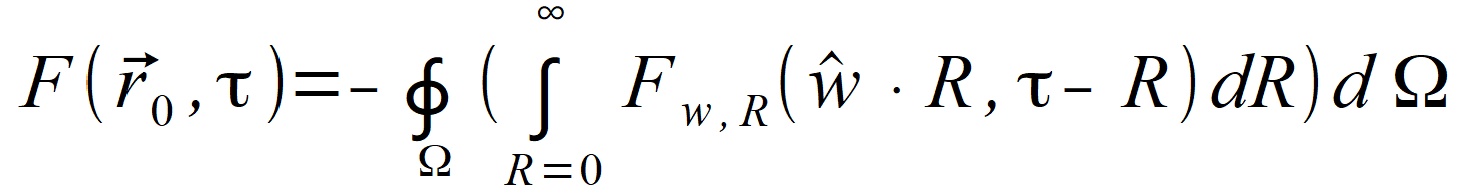	(2.91)
lub
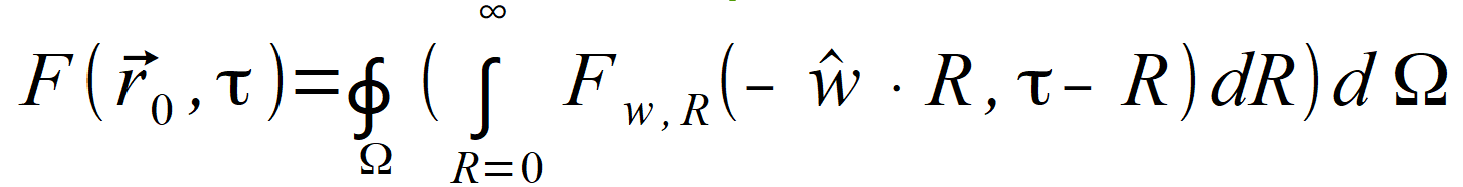	(2.92)
Wielkość F ( r₀⃗ , τ ) jest wektorem i właściwymi wzorami będą
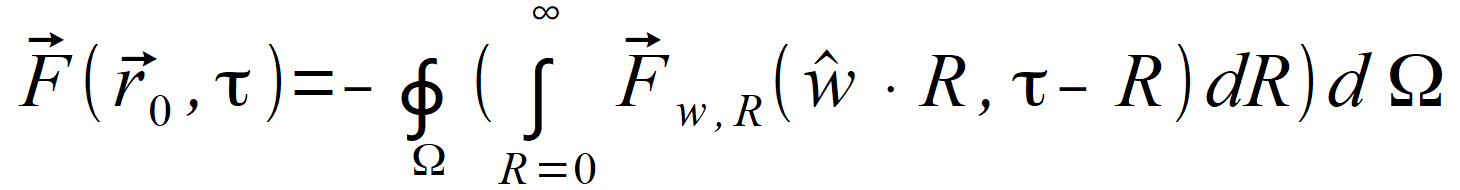	(2.93)
lub
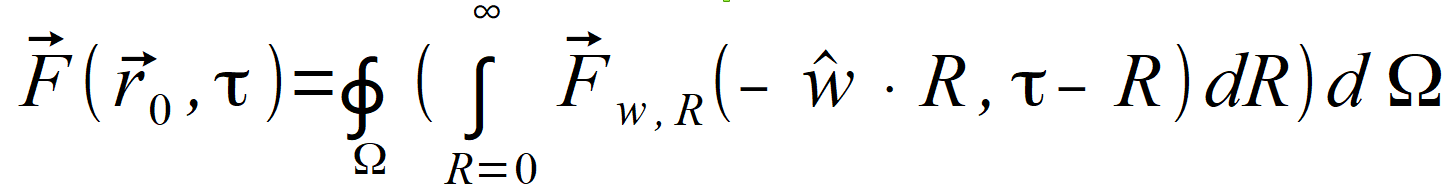	(2.94)