HenrykDot

★ HenrykDot.com ★
jest stroną towarzyszącą serii książek wydawanych przez AIUT pod wspólnym glównym tytułem
"Fizyka Mojej Urojonej Czasoprzestrzeni", których autorem jest Henryk Dot.

ENGLISH

Strona główna

Fizyka 3 - Maxwell
Od autora
Spis treści
O czym jest ta książka
Fragmenty historii
Elementy nowe
Całkowicie błędne
Elementy błędne

Fizyka 3 - Rozdzial 1
Równania
Zespolone pole E i B
Dalsze uogólnienie
Rozwiązanie ogólne

Fizyka 3 - Rozdzial 2
Rozwiązania równań
Warunki początkowe
Równanie niejednorodne
Rozw. dla trzech kierunków
Cztery prawa fizyki

Fizyka 3 - Dodatek
Dowód Fermata
Przypuszczenie Beala
Trójki pitagorejskie
Masa inercyjna
Stała grawitacji big G
Gdzie patrzy Księżyc

Fizyka 3 - Zakończenie
Zakończenie

Fizyka 4 - Przejście do Fizyka 4
Otwarcie nowej książki

Książki wydawane przez AIUT znajdują się
w bibliotekach zgodnie z listą egzemplarzy obowiązkowych.

Drugie wydanie "Fizyka 3"
ISBN 978-83-926856-1-6
Fizyka

można kupić w Warszawie
w Księgarni Akademickiej
Oficyny Wydawniczej PW
ul.Noakowskiego 18/20

oraz w Katowicach
w księgarni "Liber"
ul. Bankowa 11.
(teren Uniwersytetu Ślaskiego)

Wydanie angielskie "Physics"
ISBN 978-83-926856-2-3
Fizyka

jest również w bibliotekach
a o sposób dystrybucji należy pytać wydawca@aiut.com.


2.3.3. Poprawna interpretacja zależności od kwadratu odległości W równaniach Maxwella łatwo dostrzec prawa Ampera, Faraday'a oraz niekompletne prawo Biota-Savarta. Kompletne prawo Biota-Savarta oraz prawo Coulomba są widoczne dopiero w rozwiązaniach. Szczególną właściwością przedstawionych rozwiązań jest pokazanie, że zależność od kwadratu odległości nie jest związana z ograniczeniami (wymaganiami) na przykład aby pole w twierdzeniu Gaussa wokół ładunku było równomierne (jednakowe we wszystkich kierunkach) czy, że te prawa są słuszne w otoczeniu za wyjątkiem punktu R=0. Ograniczenia te były zasygnalizowane w punkcie „W.5. Elementy niewłaściwie interpretowane”. Poszukujemy rozwiązań, które nie są związane z wymienionymi ograniczeniami. Zamieniając kolejność całkowania we wzorze (2.93)
		(2.95)
możemy całkowanie po kącie sferycznym Ω zamienić na całkowanie po całej powierzchni kuli o konkretnym promieniu R. Traktując elementarny kąt sferyczny dΩ jako iloczyn dwóch elementarnych kątów na prostopadłych kierunkach
i		(2.96)
(gdzie da i db są elementarnymi fragmentami okręgów o promieniu R, znajdującymi się na kołach - pionowym oraz poziomym) wzór (2.95) przybiera postać
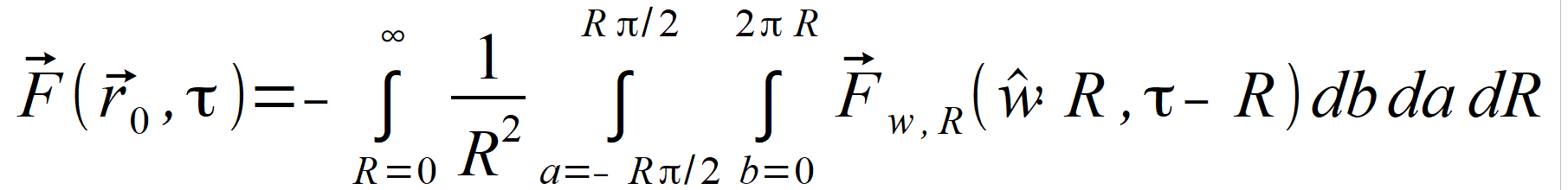
		(2.97)
Fragmenty okręgów da i db oraz promień R zaznaczone są na rysunku (Rys.4). Łuki a i b pokazane na pionowym i poziomym kole reprezentują odpowiednio kąty α = a/R i β = b/R , które są projekcją wectora R na płaszczyznę XY oraz pozycją wectora R względem płaszczyzny XY, gdzie w _x = cos( b/R) · cos( a/R), w _y = sin( b/R) · cos( a/R) oraz w _z = sin( a/R).

x a da R
Rys.4.
Zależność od odwrotności kwadratu odległości jest efektem całkowania po całej warstwie o grubości dR kuli o promieniu R.


2.3.4. Prawo Biota-Savarta w równaniach Maxwella
Rozwiązanie równania niejednorodnego zaczniemy od pola magnetycznego, gdzie mamy tylko jeden rodzaj źródła
.	(2.98a)
Dla większej przejrzystości wzorów obliczenia prowadzić będziemy dla natężenia pola magnetycznego H, którego źródło oznaczymy
.	(2.98)
Poszczególne składowe tego źródła mają wartości:
,	(2.99a)
,	(2.99b)
.	(2.99c)
Poszczególne składowe tego źródła mają wartości:
,	(2.100)
.	(2.101)
Poszczególne składowe tego źródła mają wartości:
,	(2.102a)
.	(2.102)
Poszczególne składowe tego źródła mają wartości:
,	(2.103a)
,	(2.103b)
.	(2.103c)
co jest równoważne
.	(2.104)
Wstawiając to do (2.97), otrzymujemy odpowiednik prawa Biota-Savarta, który dodatkowo uwzględnia opóźnienia fali związane z odległością
.	(2.105)

2.3.5. Prawo Coulomba w równaniach Maxwella
Prawa strona równania dla pola elektrycznego (1.46) ma dwa składniki
.	(2.106)
Dla pierwszego z nich
	(2.107)
całki (2.100) i (2.101) są bardzo łatwe, bo
	(2.108)
i wykorzystując (2.108) we wzorze (2.97). otrzymujemy
,	(2.109)
który jest odpowiednikiem prawa Coulomba, gdzie
	(2.110)
jest elementarnym ładunkiem elektrycznym dq, w elementarnej jednostce objętości dV = da db dR , znajdującym się w miejscu (r +w R, τ - R ) przestrzeni V. Mimo że wzór (2.110) jest ogólniejszy od prawa Coulomba, bo dopuszcza zmienność ładunku w czasie, to jednak nie oznacza uwzględniania ruchu tego ładunku. Ma on zastosowanie, kiedy odległe ładunki pozostają w tym samym miejscu przez czas τ > R.

2.3.6. Prawo indukcji Faradaya w równaniach Maxwella
Drugim składnikiem dla pola elektrycznego w (2.106) jest
	(2.111)
i jest to najbardziej znaczące źródło pola elektrycznego. Potrzebna dla

całka ma postać
	(2.112)
Całka (2.112) stosownie do (2.58) i (2.59) ma być realizowana dla stałego τ = - R , co powoduje, że nie jest możliwe określenie pochodnej względem czasu dla tego kierunku. Można to uczynić dla kierunku prostopadłego do w. Składowa pochodnej gęstości prądu względem czasu na kierunku prostopadłym do w jest równa
,	(2.112a)
co powoduje, że całka (2.112) przyjmuje postać
	(2.113)
Ostatecznie możemy według (2.97) napisać dla pola pochodzącego od najbardziej ogólny wzór
	(2.114)
Prawo Faradaya w równaniach Maxwella jest zawarte już w równaniu ale jego właściwe funkcjonowanie wyraża wzór (2.114).