HenrykDot

★ HenrykDot.com ★
is the online companion to a series of books published by AIUT under the common main title
"Physics of My Imaginary Space-Time" by Henryk Dot.

POLSKI

last update
20/01/2023

Home

Physics 3 - Maxwell
Note from the Author
Table of Contents
What is this book
Historical facts
New aspects
Fully erroneous
Incorrectly interpreted

Physics 3 - Chapter 1
Equations
Complex vectors form
The Most General form
The General Solution

Physics 3 - Chapter 2
Solutions
Initial conditions
Non-homogeneous equation
Solution for three-directions
The four laws

Physics 3 - Supplement
Fermat's proof
Beal's conjecture
Pythagorean triples
Inertial mass
Gravity constans big G
What does the Moon look at?

Physics 3 - Final notes
Final notes

Physics 4 - New book
Entry

Books published by AIUT
are found in libraries according to the list of compulsory copies.

Second Edition of "Fizyka 3"
ISBN 978-83-926856-1-6
Fizyka

can be bought in Warsaw
in the Academic Bookstore
PW Publishing House
Noakowskiego street 18/20

and in Katowice
in the bookstore "Liber"
Bankowa street 11.
(area of Silesian University)

English edition of "Physics"
ISBN 978-83-926856-2-3
Fizyka

is also in libraries
and the distribution method should be asked wydawca@aiut.com.


2.3.3. Correct interpretation of inverse square law Laws of Ampere, Faraday, and partial Biot-Savart’s law can be easily found in Maxwell’s equations. The complete Biot-Savart’s law as well as Coulomb’s law can be seen only in solutions.. The specific feature of solutions presented in this book is to show that inverse square (distance) relation is independent of any requirements of limitations. The examples of such imposed requirements are for instance: field around charge in Gauss’ theorem should be uniform (identical in all directions) or that laws are applicable to whole area except the point where R=0. Such limitations were already pointed out in paragraph I.5 – “Incorrectly interpreted specific problems”. We are searching then for solutions which do not depend on limitations listed above. By changing the order of integration in equation (2.93),
		(2.95)
we can change the integration by spherical angle Ω to integration on whole surface of a sphere having specific radius = R. Elementary spherical angle dΩ can be treated as a product of two elementary angles in perpendicular directions.
and		(2.96)
(where da and db represent elementary sections located at vertical and horizontal circles with radius R, ). Formula (2.95) then takes a form of:
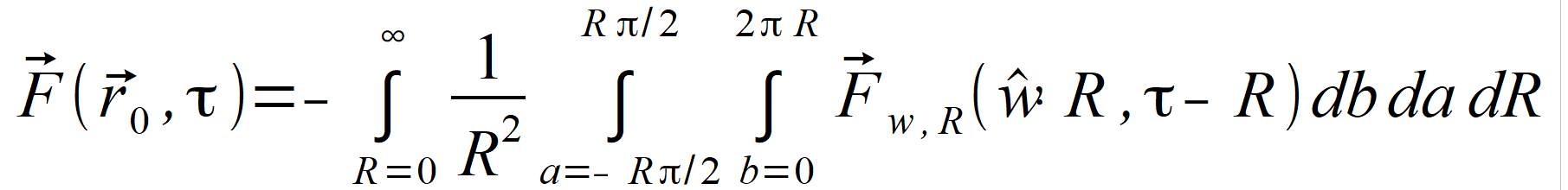
		(2.97)
Sections of circles da and db and radius R are depicted on the drawing (Fig. 4). The arcs a and b shown on vertical and horizontal circles represent the angles α = a/R and β = b/R respectively, showing the projection of the vector R onto the XY plane and the position of the vector R relative to the XY plane - and determine accordingly: w _x = cos( b/R) · cos( a/R), w _y = sin( b/R) · cos( a/R) and w _z = sin( a/R).

x a da R
Fig.4
The dependence on the inverse square of the distance results from the integration over the entire layer of thickness dR on a sphere with radius R.


2.3.4. Biot- Savart’s law in Maxwell’s equations
We begin the solution of nonhomogeneous equation with definition of magnetic field where we have only one kind of source:
.	(2.98a)
For sake of better clarity of equations, in further calculations we will use magnetic field strength, so its source is denoted as:
.	(2.98)
Individual components of this source are:
,	(2.99a)
,	(2.99b)
.	(2.99c)
In order to calculate integrals in equations:
,	(2.100)
.	(2.101)
first, we calculate integral:
,	(2.102a)
.	(2.102)
Integrating (2.99) using the same approach as in (2.102) and applying relation note used for formula (2.90), we obtain:
,	(2.103a)
,	(2.103b)
.	(2.103c)
which is equivalent to:
.	(2.104)
By inserting it into (2.97), we obtain equivalent of Biot-Savart’s law, which in addition takes wave time lag (related to distance) into account.
.	(2.105)

2.3.5. Coulomb’s law in Maxwell’s equations
Right side of the equation for electric field (1.46) consists of two components:
.	(2.106)
For first one:
	(2.107)
Integrals (2.100) and (2.101) are quite easy to use since
	(2.108)
nd using (2.108) in formula (2.97). we obtain:
,	(2.109)
which is equivalent to Coulomb’s law, where:
	(2.110)
represents elementary electric charge dq, in elementary volume unit dV = da db dR , which is located in place of (r +w R, τ - R ) in V space. The formula (2.110) is more general than Coulomb’s law since it allows for electrical charge variation in time, which does not mean that it takes into account any movement of this charge. It is applicable when remotely located charges remain in the same place for time τ > R.

2.3.6. Faraday’s induction law in Maxwell’s equations
The second component of electric field in (2.106):
	(2.111)
represents the most significant source of electric field. The integral needed to determine:

takes the form of:
	(2.112)
Integral (2.112) according to (2.58) and (2.59) has to executed for constant τ = - R , thus it is not possible to determine a derivative in respect to time for this direction. However, this can be done for a direction perpendicular to w. The current density component in respect to time in the direction perpendicular to w is equal to:
,	(2.112a)
which results in the following form of integral (2.112):
	(2.113)
Finally, per formula (2.97) for field originating from we can derive the most general formula:
	(2.114)
Faraday’s law in Maxwell’s equations, is in fact already included in: but its real functionality is expressed in formula (2.114).