HenrykDot

★ HenrykDot.com ★
is the online companion to a series of books published by AIUT under the common main title
"Physics of My Imaginary Space-Time" by Henryk Dot.

POLSKI

last update
20/01/2023

Home

Physics 3 - Maxwell
Note from the Author
Table of Contents
What is this book
Historical facts
New aspects
Fully erroneous
Incorrectly interpreted

Physics 3 - Chapter 1
Equations
Complex vectors form
The Most General form
The General Solution

Physics 3 - Chapter 2
Solutions
Initial conditions
Non-homogeneous equation
Solution for three-directions
The four laws

Physics 3 - Supplement
Fermat's proof
Beal's conjecture
Pythagorean triples
Inertial mass
Gravity constans big G
What does the Moon look at?

Physics 3 - Final notes
Final notes

Physics 4 - New book
Entry

Books published by AIUT
are found in libraries according to the list of compulsory copies.

Second Edition of "Fizyka 3"
ISBN 978-83-926856-1-6
Fizyka

can be bought in Warsaw
in the Academic Bookstore
PW Publishing House
Noakowskiego street 18/20

and in Katowice
in the bookstore "Liber"
Bankowa street 11.
(area of Silesian University)

English edition of "Physics"
ISBN 978-83-926856-2-3
Fizyka

is also in libraries
and the distribution method should be asked wydawca@aiut.com.


2.3. Solutions for three-directional equation 2.3.1. Solution for three-directional homogenous equation For three dimensions, instead of we apply ,
.	(2.76)
Perhaps nabla (del) operator squared also called Laplacian, unjustifiably scared some people interested in solution of Maxwell’s equations. We can find in related publications various attempts to solve these equations, mainly based on simplifications or on imposing additional conditions. Paul Dirac asked his coworker “Is your thinking algebraic or geometrical?”. Richard Feynman similarly treated comprehension – he stated that to understand a problem means when looking at equation, one cannot see its algebraic transformations but its solution. Let’s then look “geometrically” at equation (2.76). Without sacrificing details, we can skip vector sign over F and analyze this form:
.	(2.77)
Equation (2.77) describes the behavior of function in point without any sources at this point, which is depicted on Fig.3.

Y r F3 F2 F1 /div>
Fig.3
Notations on the drawing x, y, z – coordinate system r - position vector for analyzed point F1, F2, F3 – example of waves (denoted by double arrow) solid line denoted waves passing through the point, broken line denotes fragments of the same waves which are not passing through the point Homogenous wave equation (2.77) contains all possible waves passing through point , generated in points where equation (2.1) includes wave sources. Both parts of equation (2.77) contain in themselves a sum of possible waves while the quantity of these waves in general case is determined by quantity of sources which can be continuously distributed in space. Since this is a linear differential equation, this equation must be satisfied by sum of all waves as well as by each of individual waves. This allows us to deal only with single wave (i.e. single solution) which passes through any given point at any selected one-direction e.g. assuming that wave source is at this direction). Direction can be expressed as: wˆ = w_x∙ xˆ + w_y∙ yˆ + w_z∙ zˆ , where wˆ , xˆ , yˆ , zˆ – unit vectors w_x ,w_y ,w_z – unit vectorcomponents, wˆ , which satisfy relation: w_x² + w_y² + w_z² = 1 . Denoting the position of analyzed point by r₀⃗ , for pencil of lines passing through this point we can then express all position vectors as r⃗ = r⃗ ₀ + ξ ∙ wˆ and corresponding value of the function as
.	(2.78)
For defined r₀⃗ and wˆ we will use short form F(r⃗ , τ ) = F_ξ ( ξ , τ ) remembering that function F_ξ ( ξ , τ ) is determined for specifically defined parameters r₀⃗ and wˆ . We will introduce one more variable R and its vector equivalent variable R⃗ = wˆ ∙ R , which will be used in further formulas. Using new notations, we have 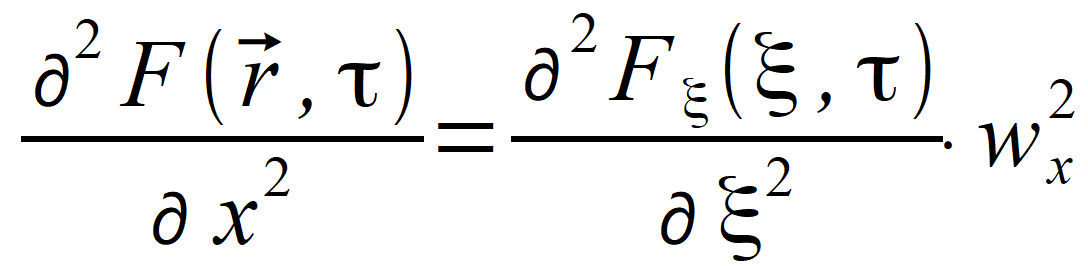, ,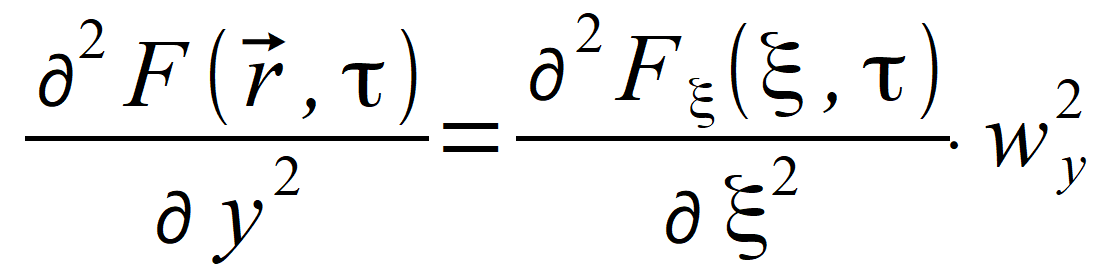 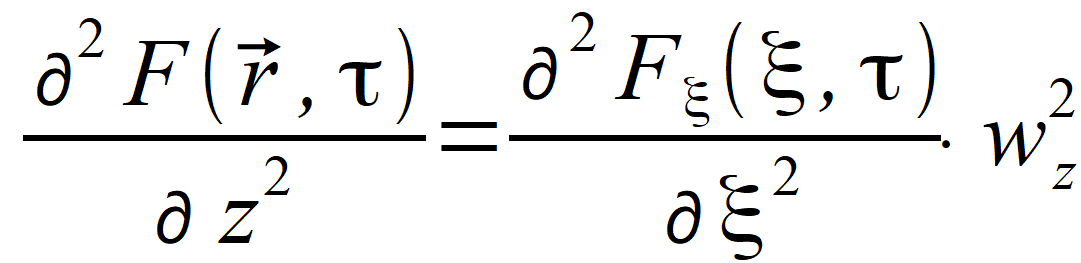. So, we can see that
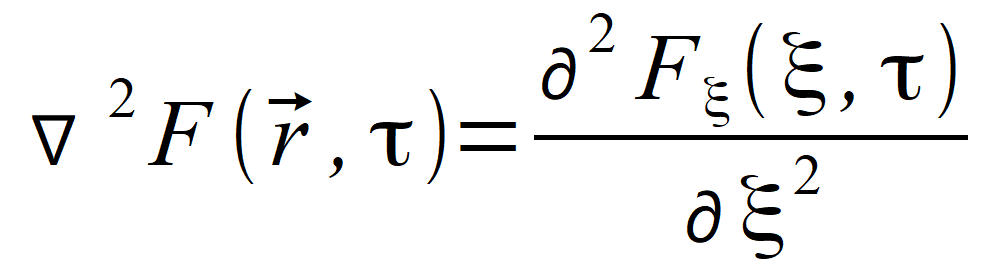	(2.79)
Thus, our three-directional equation became one-directional equation, already well worked out:
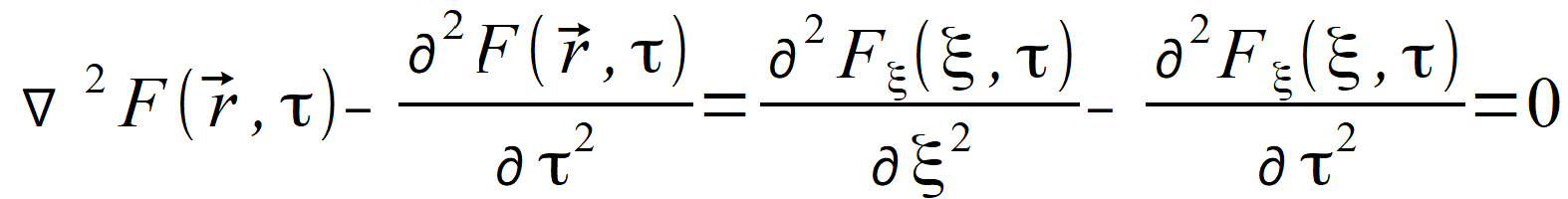	(2.80)
for which we can determine solutions. When we can see that a solution is independent of other dimensions, we usually assume that this one-directional solution is represented by planewave. The solution of an equation in the form of F_ξ ( ξ , τ ), exhibits several similar features, but it cannot be considered as a planewave since it only determines course of a function on straight line ξ ∙ wˆ passing through the point r⃗ ₀ . In order to obtain value of the function in point r⃗ ₀ , we must sum up all solutions at all directions wˆ passing through point r⃗ ₀ . If we denote elementary spherical angle as dΩ, then using radian measure of angle we obtain
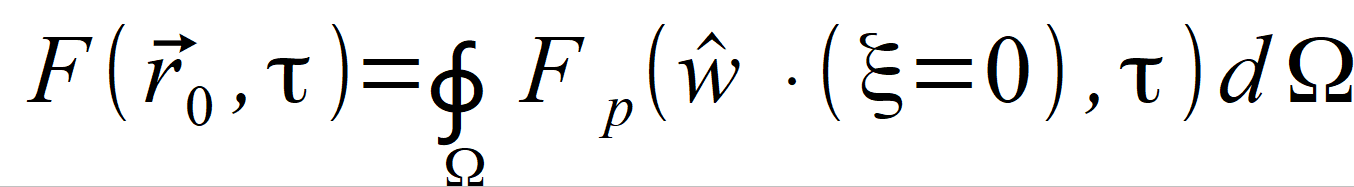	(2.81)
Subscript index p in the notation of function F_p ( wˆ ∙ ξ , τ ) represents incoming wave from direction wˆ , thus we need to consider influence of direction in determining function F_p ( wˆ ∙ ξ , τ ). For Maxwell’s equations the value of F_p ( wˆ ∙ ξ , τ ) represents vector and integral equation is expressed in following form:
	(2.82)
2.3.2. Solution for nonhomogeneous equation The relations (2.80) and (2.82) allow us for deriving the solution of nonhomogeneous equation for three directions. Complementing equation (2.80) with forcing functions f ( r⃗ , τ ) which appear in (2.1) and which act only in chosen direction, i.e. f_{w, ξ} ( wˆ ∙ ξ , τ ) we obtain the equation:
	(2.83)
for which similarly to (2.74) and (2.75) we can formulate following solutions:
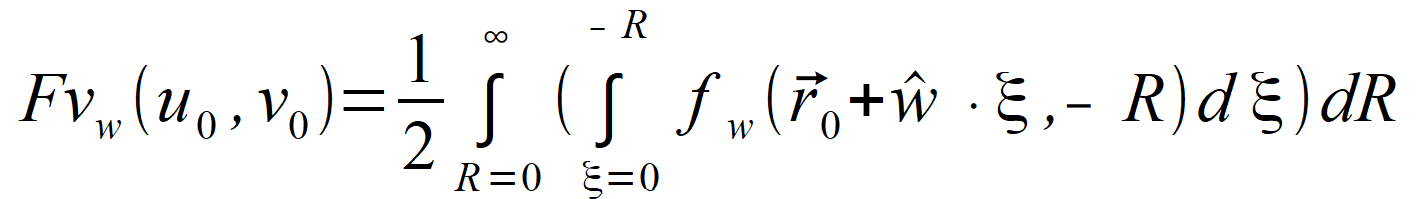	(2.84)
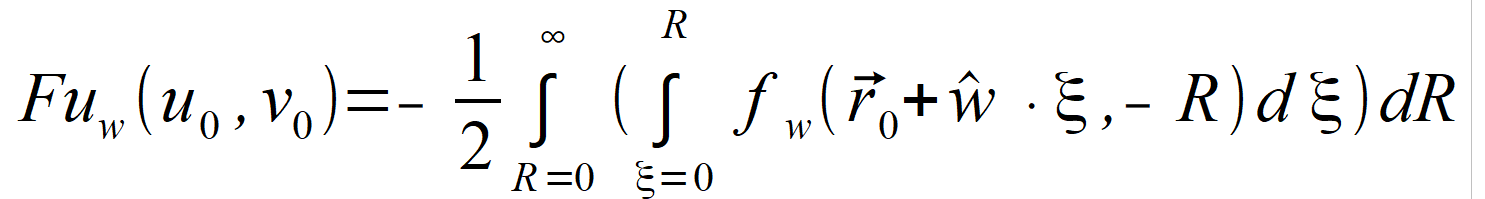	(2.85)
To indicate that functions f ( r⃗ , τ ) , Fv and Fu are related only to chosen direction, we assign to them subscript w . The same applies to function Fo from formula (2.69) therefore, we obtain:
Fo_w ( u₀ , v₀ ) = Fv_w ( u₀ , v₀ ) + Fu_w ( u₀ , v₀ )	(2.86)
Inner integrals in equations (2.84) and (2.85) depend only on R. Denoting Fo_{w, R} () as their indefinite integrals:
	(2.87)
equations (2.84) and (2.85) can be written as
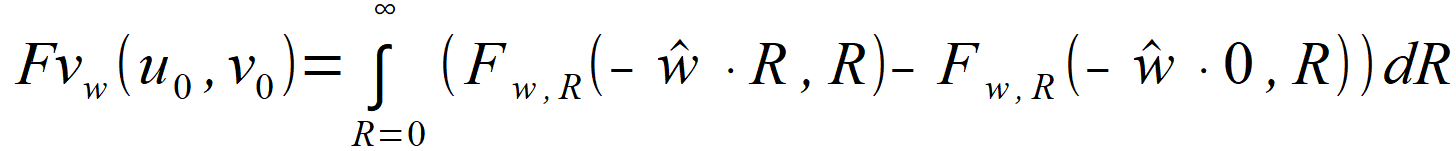	(2.88)
	(2.89)
and after applying (2.86) we have:
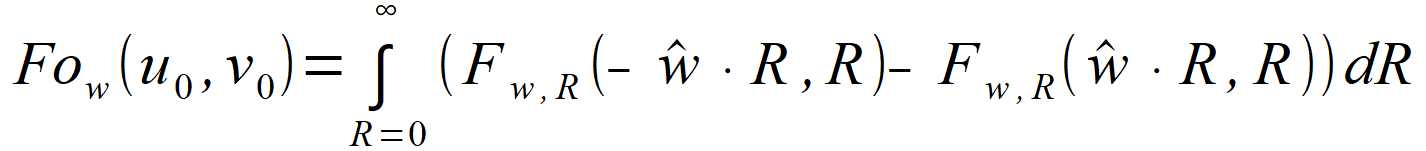	(2.90)
Fo_w ( u₀ , v₀ ) in equation (2.90) corresponds to F_p ( r⃗ ₀ + wˆ ∙ ( ξ = 0 ) , τ) in equation (2.81). It can be noted that 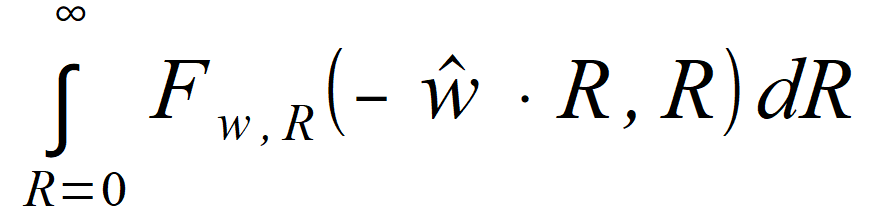and 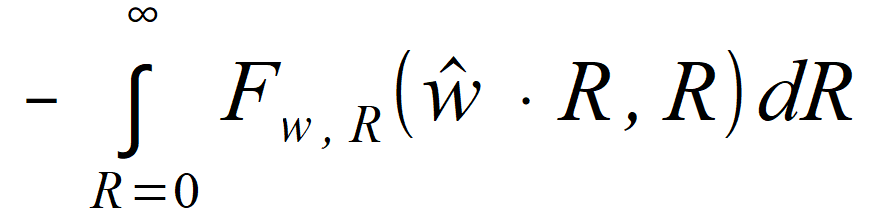represent waves coming from opposite directions. Also, integral of waves incoming from all directions is a sum of integrals on the same hemisphere 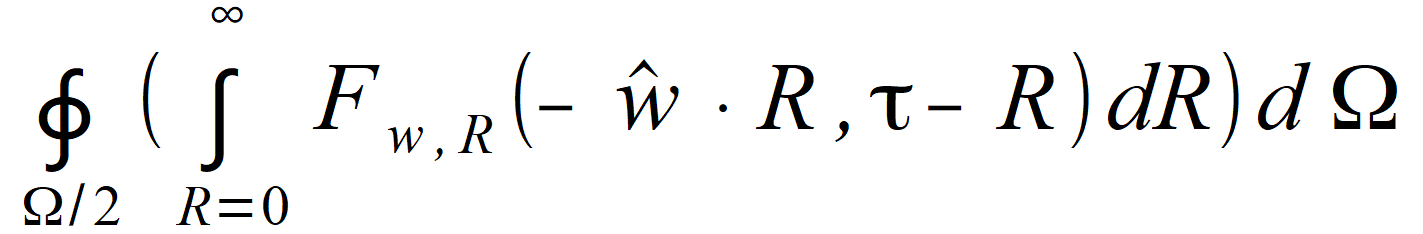for first hemisphere 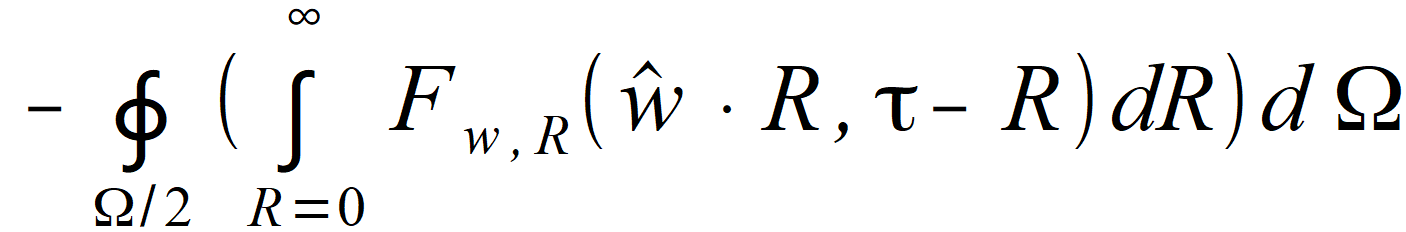or second hemisphere. Reversal of directions, thus change of w to -w is equivalent to change of integration sign. The sum of both of these integrals can be obtained by integrating on whole sphere using one of the formulas below:
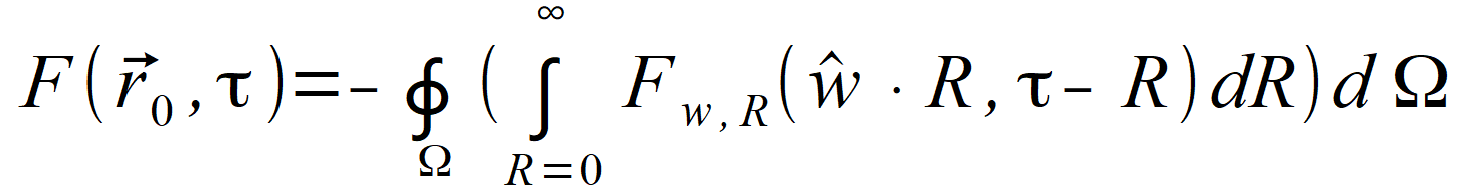	(2.91)
or
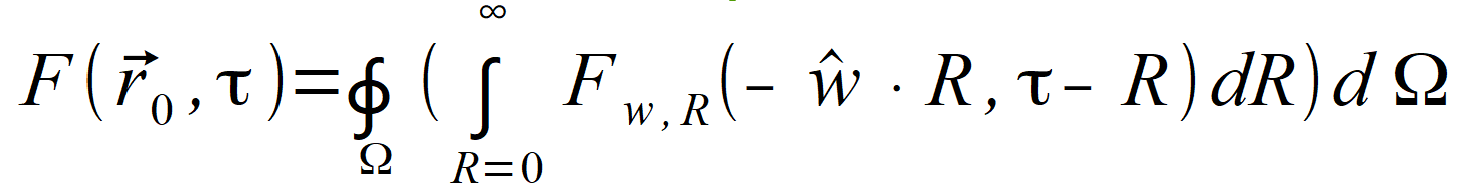	(2.92)
Value F ( r₀⃗ , τ ) represents a vector, so correct equations are:
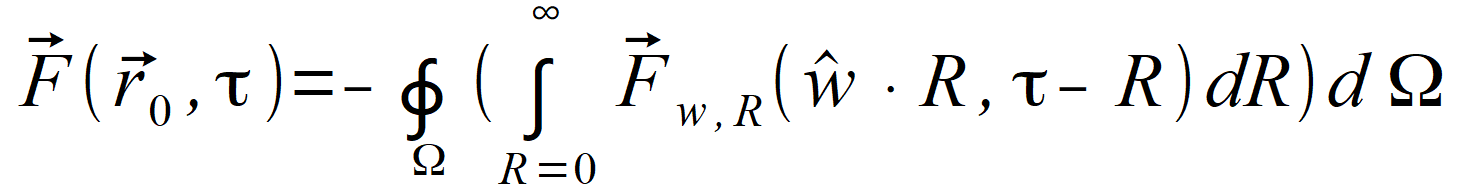	(2.93)
or
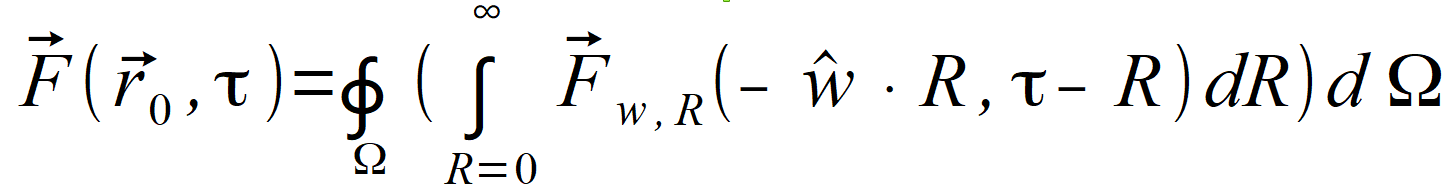	(2.94)